Systems of linear Equations: Explained with Methods for Finding Solutions

Published by Jessica Helen in Teaching Tips · 13 April 2023
Tags: maths, numbers, methodology, articles

$Math teachin tips$

Solving a system of linear equations has multiple methods available to find the solution. These methods include substitution, cross-multiplication, elimination, and more. However, we will focus on the elimination method and substitution method only.

The elimination and substitution methods will be covered in this article, and the reader will learn how to use these techniques to solve a system of linear equations. Further, we will provide step-by-step solutions to several examples using both methods.

What is the system of linear equations?

A linear equation is an algebraic equation where the highest power of each variable is one. The general form of a linear equation with two variables is ax + by = c, where a, b, and c are constants. A system of linear equations is a collection of two or more linear equations that involve the same variables, and solving them to find a set of values that make all the equations in the system accurate.

Methods for Finding Solutions of linear equations

1. Elimination method

The elimination method is a technique used to determine the solution of the system of linear equations. The coefficient of one variable in both equations should be equal in this method. Eliminate one variable by adding or subtracting the equations. This results in a new equation with only one variable, which can be solved easily.

The value of this variable can be used to determine the value of the other variable in the given system. The elimination method considers more efficient when the coefficient of the variables are relatively simple.

Solving the system of linear equations by elimination method

We will explore the process of solving a pair of linear equations by the elimination method.

Multiply one or both of the equations by any suitable non-zero constant, such that one variable’s coefficient in both equations becomes equal.
Check out the sign of the equal coefficient. If they have similar signs, subtract the system of linear equations. Add a system of linear equations if they have opposite signs.
Here, one variable will be eliminated, and calculate the value of other variables.
Put this value in any given equation to get the value of another unknown variable.
Check the solution by putting the values of both variables into the system of linear equations to make sure the equation is satisfied.

Example

Solve the following system of linear equations using the elimination method

x + 2y = 3

2x + y = 6

Solution

Given the system of linear equation

x + 2y = 3_____ (i)

2x + y = 6_____ (ii)

Step 1. In the first step, we equate the coefficient (either variable x or y). To equate the coefficient of y, multiply equation (ii) by 2. We have

4x + 2y = 12_____ (iii)

Step 2. The coefficient of variable y is equal in equation (i) and equation (iii), but they have a similar sign, so subtract equation

(i) from (iii)

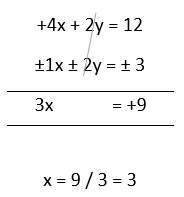
x = 3

Step 3. Put x = 3 in equation (i) i.e.

3 + 2y = 3

Step 4. Simplify the equation

3 + 2y = 3

2y = 3 – 3

2y = 0

y = 0 / 2 = 0

y = 0

So, x = 3, and y = 0 are the required solution of the given system of linear equations.

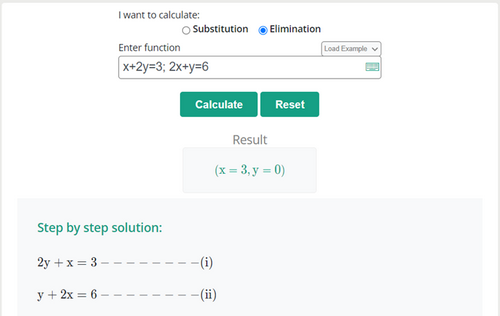
A system of equations calculator is a helpful way to solve system of linear equations with steps to get rid of lengthy calculations by manual method.

$math teaching tips$

2. Substitution method

The substitution method is a useful mathematical tool to determine a set of linear equations by solving one equation for the value of one variable in terms of the other variables, and then putting this value into the other given equation. A new equation with a single variable, which can be easily computed, is produced by this step.

To determine the value of another variable, substitute the computed value back into any given equation.

Using the substitution method to find the solution of a linear equation

To determine the system of linear equations by substitution method, follow the given steps.

Determine the value of one variable in terms of other variables.
Substitute this expression into the other equation, creating a new equation with a single variable.
After obtaining the new equation, solve it to determine the value of one of the variables.
Put the value of the solved variable into another equation to get the value of other variables.
In order to confirm the solution, substitute the values of both variables into the system of linear equations to make sure the equation is satisfied.

Example

Solve the following system of linear equations by the substitution method

x + 2y = 3

2x + y = 6

Solution

x + 2y = 3_____ (i)

2x + y = 6_____ (ii)

Step 1. Determine the value of one variable (either x or y) in terms of other variables from any given equation.

From equation (ii), we get

y = 6 - 2x

Step 2. Put this value in equation (i), and we have

x + 2 (6 - 2x) = 3

x + 12 - 4x = 3

12 - 3x = 3

- 3x = 3 - 12

- 3x = - 9

x = - 9 / - 3 = 3

x = 3

Step 3. Put x = 3 in equation (i) i.e.

3 + 2y = 3

2y = 0

y = 0 / 2

y = 0

Hence, x = 3, and y = 0 are required solutions.

Conclusion

In this article, we have covered the elimination and substitution methods, for solving a system of linear equations. We described steps to solve the linear equation system using both methods. The choice of method depends on the nature of the given equations. Further, we solved some examples by using both methods.

It is essential to practice solving problems using both methods to better understand of linear equations and improve problem-solving skills.

Author Bio

Jessica Helen is a highly experienced and passionate mathematician. Jessica Helen is not only an expert in her field, but she is also a natural educator, making even the most complex mathematical concepts approachable and engaging for students and enthusiasts alike. His unique writing style blends clarity and simplicity, making her blog a go-to resource for students, educators, and math enthusiasts worldwide.

There are no reviews yet.